벡터(Vector)란?
벡터는 크기와 방향을 동시에 가지는 수학적 개념이다.
Unity에서의 쓰임
오브젝트의 위치 방향, 속도 등을 표현할때 벡터를 사용한다.
오브젝트의 위치(Position) 벡터
transform.position = new Vector3(0, 1, 2);방향(Direction) 벡터
어디를 바라보는지 알려주는 단위 벡터
Vector3 forward = transform.forward;속도(Velocity) 벡터
방향과 속도를 가진 벡터로 표현되며 움직임을 구현할때 주로 사용한다.
Vector3 velocity = new Vector3(1, 0, 0); // 오른쪽으로 1만큼 이동하는 속도
transform.position += velocity * Time.deltaTime;벡터의 구성 요소
크기(Magnitude)
벡터의 길이를 의미한다. 보통 얼마나 힘/속도를 가지는지를 판단하는 데 사용된다.
Unity에서는 vector.magnitude를 사용해서 구할 수 있다.
Vector3 move = new Vector3(3, 4, 0);
float length = move.magnitude; // 5 (3-4-5 삼각형)방향(Direction)
벡터가 어느 방향을 향하는지 나타내며 방향만 따질 때는 보통 단위 벡터로 정규화한다.
Vector3 direction = move.normalized;벡터 덧셈과 뺄셈
벡터는 단순한 수치가 아니라 공간상에서 방향과 거리를 가진 값이다. 따라서 두 벡터를 더하거나 빼면 새로운 위치나 방향을 계산할 수 있다.
벡터 덧셈
두 벡터를 더하면 각 축 방향의 값을 더한 새로운 벡터가 된다.

Unity에서는 오브젝트 사이의 중간 위치를 구하거나 여러 힘의 합을 표현할 때 사용한다.
Vector3 A = new Vector3(0, 0, 0);
Vector3 B = new Vector3(4, 0, 0);
Vector3 midpoint = (A + B) / 2; // (2, 0, 0)벡터 뺄셈
두 벡터를 빼면 벡터 A - B 는 "B에서 A까지 가는 방향과 거리"를 의미한다.
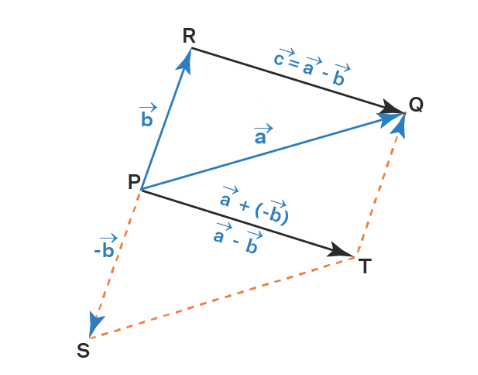
Unity에서는 적이 플레이어를 추적하거나, 미사일이 목표를 향해 날아갈 때 자주 사용된다.
실습: 벡터를 사용하여 두 오브젝트 간의 거리와 방향 구하기
Vector3 playerPos = new Vector3(1, 0, 1);
Vector3 enemyPos = new Vector3(5, 0, 1);
Vector3 toPlayer = playerPos - enemyPos; // (-4, 0, 0)
float distance = toPlayer.magnitude; // 4(적과 플레이 사이의 거리)
Vector3 direction = toPlayer.normalized; // (-1, 0, 0) (플레이어가 적을 향하는 방향)스칼라(Scalar)란?
스칼라는 방향이 없는 수치값, 즉 크기만 존재하는 물리량을 의미한다. 벡터와는 다르게 방향이 없기 때문에 단순히 양이나 양의 정도를 표현할 때 사용된다.
Unity에서는 체력, 속력, 거리 등 다양한 수치 정보를 나타낼 때 사용된다.
속력 (Speed) - 오브젝트가 얼마나 빠른지
float speed = 5.0f;
체력 (HP) - 캐릭터의 생명력 수치
int hp = 100;
거리 (Distance) - 두 지점 간 떨어진 거리
float d = Vector3.Distance(A, B);
점수 (Score) - 게임의 정량적 결과 값
int score = 1500;벡터와 스칼라의 관계
벡터의 크기는 스칼라다. 따라서 velocity.magnitude 는 스칼라 값입니다.
Vector3 velocity = new Vector3(3, 4, 0);
float speed = velocity.magnitude; // 결과: 5.0 (스칼라)스칼라를 벡터에 곱하면 방향은 유지되고 크기만 조절된다. 이걸 통해 이동 속도, 힘의 크기 조절 등을 할 수 있다.
ector3 direction = new Vector3(1, 0, 0); // 방향만 있는 단위 벡터
float speed = 5.0f; // 스칼라
Vector3 velocity = direction * speed; // 결과: (5, 0, 0)
실습 1 : 속도 벡터 만들기
Vector3 direction = new Vector3(1, 0, 0); // 오른쪽 방향 (단위 벡터)
float speed = 5.0f; // 속력 (스칼라)
Vector3 velocity = direction * speed; // (5, 0, 0)
실습 2 : 캐릭터 움직이기
void Update()
{
Vector3 moveDir = new Vector3(Input.GetAxis("Horizontal"), 0, Input.GetAxis("Vertical"));
float moveSpeed = 3.0f; // 속력은 스칼라
transform.position += moveDir.normalized * moveSpeed * Time.deltaTime;
}단위 벡터(Unit Vector)란?
단위 벡터는 크기(Magnitude)가 1인 벡터이다. 방향은 유지하되 길이만 1로 고정된 벡터로 방향만 필요할 때 사용된다.
Vector3 A = new Vector3(3, 4, 0);
float magnitude = A.magnitude; // 크기: 5.0
Vector3 unitVector = A / magnitude; // (0.6, 0.8, 0)
Debug.Log("단위 벡터: " + unitVector);
// Vector3 unitVector = A.normalized; 요렇게도 가능왜 단위 벡터가 중요한가요?
게임에서 오브젝트를 움직이거나 회전시킬 때 방향과 속도를 분리해서 다루는 것이 일반적이다. 이때 방향과 속도를 분리하는 것이 중요한 이유는 다음과 같다.
1) 방향을 따로 관리 가능
방향만 필요할 때 크기는 의미가 없다.
2) 속도를 쉽게 조절할 수 있음
정규화된 벡터에 스칼라값을 곱하면 속도를 쉽게 조절할 수 있다.
3) 일관된 결과 보장
크기가 다른 방향 벡터를 그대로 사용할 경우 위치에 따라 속도가 달라지는 문제가 발생할 수 있다. 단위벡터는 크기가 항상 1이므로 어떤 위치든 항상 일정한 속도로 이동할 수 있다.
Vector3 direction = target.position - transform.position;
transform.position += direction * Time.deltaTime;이렇게 코드를 적을 경우 타겟이 가까워지면 천천히 멀면 빠르게 이동하면서 속도가 불균형해진다.
Vector3 unitDir = direction.normalized; // 항상 일정하게 움직임이 가능하다
transform.position += unitDir * speed * Time.deltaTime;벡터 정규화 (Normalization)
벡터 정규화는 주어진 벡터를 크기 1의 단위 벡터(Unit Vector) 로 바꾸는 과정이다. 즉 방향은 그대로 유지하고 길이만 1로 바꿔서 순수한 방향 정보만을 추출한다.
정규화가 필요한 이유
위치에 상관없이 일정한 속도 유지
사용자의 입력 벡터는 입력에 따라 크기가 달라진다. 그러므로 정규화를 하지 않으면 방향 벡터의 크기가 위치에 따라 달라지고 그만큼 이동 속도도 달라진다.
가까운 거리에서는 천천히, 먼 거리에서는 매우 빠르게 움직이게 됩니다.
transform.position += inputDir * speed * Time.deltaTime;
정규화를 통해 크기를 1로 고정하면, 항상 일정한 속도로 이동할 수 있습니다.
Vector3 moveDir = inputDir.normalized;
transform.position += moveDir * speed * Time.deltaTime;
실습 1 : 방향 제어
정규화된 벡터는 순수한 방향을 나타내기 때문에 회전이나 방향 판정에 정확하게 사용된다.
Vector3 toEnemy = (enemy.position - player.position).normalized;
Vector3 forward = player.forward;
float dot = Vector3.Dot(forward, toEnemy);
if (dot > Mathf.Cos(60f * Mathf.Deg2Rad))
{
Debug.Log("적이 시야 내에 있음");
}실습 2 : 회전 계산에 사용
정규화된 방향 벡터는 Quaternion을 이용한 회전 연산에도 필수적이다. 이를 기반으로 회전 각도를 계산하거나 방향을 지정할 수 있다.
Vector3 direction = player.position - enemy.position;
Vector3 normalizedDir = direction.normalized;
Quaternion lookRotation = Quaternion.LookRotation(normalizedDir);
enemy.rotation = Quaternion.Slerp(enemy.rotation, lookRotation, Time.deltaTime * 5);
벡터 내적(Dot Product)의 정의
내적은 두 벡터가 얼마나 같은 방향을 가리키는지 수치적으로 판단할 수 있는 연산이다. 결과는 스칼라(Scalar) 값이며 이 값의 크기와 부호를 통해 두 벡터 사이의 각도를 유추할 수 있다.
내적 공식
1) 크기 각도 기반
A ⋅ B = |A| × |B| × cos(θ)2) 좌표 기반
A ⋅ B = ax × bx + ay × by + az × bz예제 1 : 내적 계산
Vector3 A = new Vector3(3, 4, 0);
Vector3 B = new Vector3(2, 1, 0);
float dot = Vector3.Dot(A, B); // 3×2 + 4×1 + 0×0 = 6 + 4 + 0 = 10
Debug.Log("내적 결과: " + dot);
내적 값의 의미

// > 0 유사한 방향 (0~90도)
Vector3 A = Vector3.forward; // (0, 0, 1)
Vector3 B = Vector3.forward; // (0, 0, 1)
float dot = Vector3.Dot(A, B); // 결과: 1 (같은 방향)
// = 0 수직 (90도)
Vector3 A = new Vector3(1, 0, 0); // 오른쪽
Vector3 B = new Vector3(0, 1, 0); // 위쪽
float dot = Vector3.Dot(A, B); // 결과: 0 (서로 수직)
// < 0 반대 방향 (90~180도)
Vector3 A = Vector3.right; // (1, 0, 0)
Vector3 B = -Vector3.right; // (-1, 0, 0)
float dot = Vector3.Dot(A, B); // 결과: -1 (정반대)
내적을 활용한 각도 계산
θ = acos((A ⋅ B) / (|A||B|))실습
Vector3 A = new Vector3(3, 4, 0);
Vector3 B = new Vector3(2, 1, 0);
float dot = Vector3.Dot(A, B);
float angle = Mathf.Acos(dot / (A.magnitude * B.magnitude)) * Mathf.Rad2Deg;
Debug.Log("두 벡터 사이의 각도: " + angle + "도");투영(Projection)이란?
한 벡터가 다른 벡터 방향으로 얼마나 겹치는지 즉 투사된 거리를 나타낸다. 단위 벡터 B에 대해 A를 투영하면 다음과 같다.
A ⋅ B = |A| × cos(θ)이 식의 결과는 벡터 A가 벡터 B방향으로 얼마나 길게 퍼져 있는지를 나타낸다.

실습 : 경사로 방향으로 힘이 얼마나 작용하는지 크기 계산
Vector3 vectorA = new Vector3(3, 4, 0); // 원래 힘 또는 속도
Vector3 vectorB = new Vector3(1, 0, 0); // 경사면 방향 벡터
Vector3 unitVectorB = vectorB.normalized;
float projectionLength = Vector3.Dot(vectorA, unitVectorB);
Debug.Log("A가 B 방향으로 투영된 길이: " + projectionLength);벡터 외적 (Cross Product)이란?
외적은 두 벡터가 이루는 평면에 수직인 새로운 벡터를 만들어내는 연산이다. 결과는 방향과 크기 모두를 가지는 벡터이다.

A × B = (AyBz − AzBy, AzBx − AxBz, AxBy − AyBx)
외적의 결과
1) 크기
두 벡터가 이루는 평행사변형의 넓이다.

|A × B| = |A| × |B| × sin(θ)
2) 방향
결과로 나오는 벡터는 A와 B가 이루는 평면에 수직인 방향이다. 이 방향은 벡터의 순서에 따라 달라지며 좌표계의 법칙(왼손, 오른손 법칙)에 따라 결정된다.
Unity와 왼손 좌표계의 개념
이 개념은 3D 그래픽에서 회전 방향 및 벡터 연산 결과에 영향을 준다.
오른손 좌표계 : X(오른쪽),Y(위),Z(앞, 화면 안쪽)
왼손 좌표계 : X(오른쪽),Y(위),Z(뒤)
오른손 좌표계와의 차이점
오른손 좌표계에서는 z축이 화면 밖으로(뒤쪽) 향하는 반면 왼손 좌표계에서는 z축이 화면 안으로(앞쪽) 향한다. 이는 두 좌표계의 가장 중요한 차이점이다.
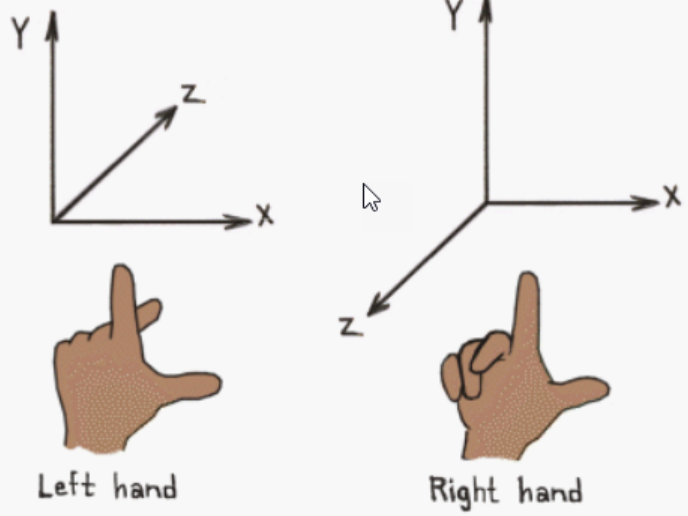
외손 좌표계에서 회전 방향은 각 축에 대해 시계 방향이다. 왼손 엄지를 회전축 방향으로 향하게 했을 때 나머지 네 손가락이 구부러지는 방향이 양(+)의 회전 방향이다.
Vector3 right = new Vector3(1, 0, 0); // 오른쪽
Vector3 up = new Vector3(0, 1, 0); // 위쪽
Vector3 forward = Vector3.Cross(right, up); // 결과는 (0, 0, 1)
벡터 외적의 활용 사례
실습 1 : 회전 방향 계산
외적을 사용하여 회전의 방향을 계산할 수 있다.
Vector3 forward = transform.forward;
Vector3 toTarget = (target.position - transform.position).normalized;
Vector3 cross = Vector3.Cross(forward, toTarget);
if (cross.y > 0) Debug.Log("오른쪽으로 회전");
else if (cross.y < 0) Debug.Log("왼쪽으로 회전");실습 2 : 법선 벡터 계산
면의 법선을 계산하여 충돌이나 물리 연산에서 면이 가리키는 방향을 구할 수 있다.
예: 3D 그래픽에서 조명 계산 시, 외적을 통해 면의 법선 벡터를 구해 빛의 반사 방향을 결정.
Vector3 AB = pointB.position - pointA.position;
Vector3 AC = pointC.position - pointA.position;
Vector3 normal = Vector3.Cross(AB, AC).normalized;
마무리 : 외적과 내적의 차이점
외적
두 벡터가 이루는 평면에 수직인 벡터를 반환한다. 이 결과 벡터는 방향과 크기를 모두 가지며 크기는 두 벡터 사이의 각도에 따라 변하고 방향은 평면에 수직이 되도록 정해진다. 외적은 주로 회전 방향을 판별하거나 삼각형의 법선 벡터를 구해 물리 충돌 방향이나 조명 계산이 사용된다.
내적
두 벡터 사이의 각도나 유사성을 계산하는 데 사용된다. 내적 값은 두 벡터가 얼마나 같은 방향을 가리키고 있는지 나타낸다. 내적이 양수일때 비슷한 방향, 0이면 수직, 음수면 반대 방향을 의미하며 주로 시야 판정이나 두 벡터 간의 각도 계산에 활용된다.
'유니티 공부 > Unity' 카테고리의 다른 글
| Unity - velocity vs addForce +) Velocity 덮어쓰기 , AddForce 무시 문제 (0) | 2025.05.22 |
|---|---|
| Unity - Lighting을 활용한 낮과 밤 시스템 구현 방법 (0) | 2025.05.19 |
| Unity - InputAction을 사용해서 플레이어 동작 기능 구현하기 (0) | 2025.05.16 |
| Unity - 제네릭이 꼭 좋은 건 아니였다. (0) | 2025.05.12 |
| Unity - FSM(Finite State Machine)을 사용해서 몬스터 AI를 만들어보자 (0) | 2025.05.09 |




댓글